 Schnittpunkte graphisch ermitteln
Schnittpunkte graphisch ermitteln
Hier erfährst du, wie Schnittpunkte von 2 Funktionen an deren Graphen bestimmt werden können.
Das Vorgehen bezieht sich auf den ti NSpire ohne CAS.
Hinweis: ein alternatives Vorgehen findest du hier:
Der Schnittpunkt dieser beiden Funktionen soll graphisch ermittelt werden.
Achte auf die Festlegung einer Funktion mit :=


Achtung: Der Schnittpunkt muss im sichtbaren Fenster liegen, sonst wird er nicht gefunden! Also: per Zoom den Bildausschnitt entsprechend wählen.
Hier passt alles, die beiden Schnittpunkte sind erkennbar.


- Graph analysieren

- Schnittpunkt

Der Taschenrechner ohne CAS analysiert nicht die Funktionen f und g mit mathematischen (algebraischen) Methoden, sondern nur die Graphen im angezeigten Bildausschnitt.
Deshalb ist anzugeben, in welchem Bereich ein Schnittpunkt zu suchen ist.
- linke Grenze des Suchbereichs ("untere Schranke") nach links verschieben
-


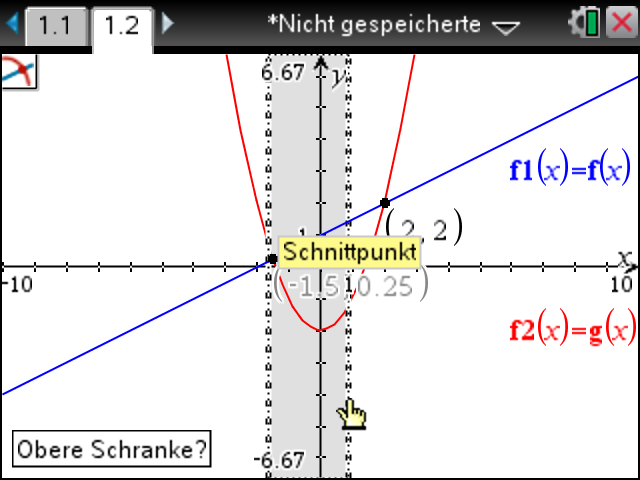
Die rechte Grenze ("obere Schranke") nach rechts verschieben (noch kein Enter!)
Es wird immer nur ein Schnittpunkt angezeigt, hier der erste ...

Wird die obere Schranke weiter nach rechts gezogen, wird der zweite Schnittpunkt markiert. Man muss sich also entscheiden: 1. oder 2. Schnittpunkt.
- Wir wählen hier den 2. Schnittpunkt:


Der zweite Schnittpunkt ist markiert und seine Koordinaten werden angezeigt.

Um auch den ersten Schnittpunkt zu markieren, muss das Verfahren erneut durchgeführt werden.
Fertig.

Praktisch ist nun: Wenn die Funktion geändert wird, ändern sich automatisch auch die gefundenen Schnittpunkte ...

Der zweite Schnittpunkt ist direkt markiert, der erste nicht. Warum fehlt der erste Schnittpunkt?
Anwort: Weil er sich nicht im zuvor festgelegten Suchbereich befindet. Die "untere Grenze" wurde bei ca. -1,7 gesetzt, der Schnittpunkt liegt aber – wie im Diagramm leicht zu erkennen ist – bei x=-2

Hinweis: ein alternatives Vorgehen findest du hier: